Mathematics

The origins of mathematics go back to the dawn of civilization in the attempts to understand the movement of the stars, to compose calendars, to keep accounts, and to measure arable land. With Ancient Greek civilization, mathematics became systematized in the form of axioms, theorems, and proofs. Science was born. Throughout history, mathematics has played a central role in culture, science, and technology. It has been widened and consolidated with the development of foundations, abstraction, and rigor, with a focus on exploring new fields and resolving new problems.
The traditional branches of mathematics are as vibrant and dynamic today as they were 50, 100, or 200 years ago. Thanks to mathematics, more and more problems can be solved, and more and more phenomena can be effectively described and analyzed.
On the other hand, we are witnessing a real explosion of new disciplines. Recent mathematical developments, coupled with the current potential of computers, have paved the way for new ways of doing science and understanding the world through developing mathematical models for highly complex phenomena, in particular through computer simulations of the behavior and evolution of the phenomena in question.

Program presentation
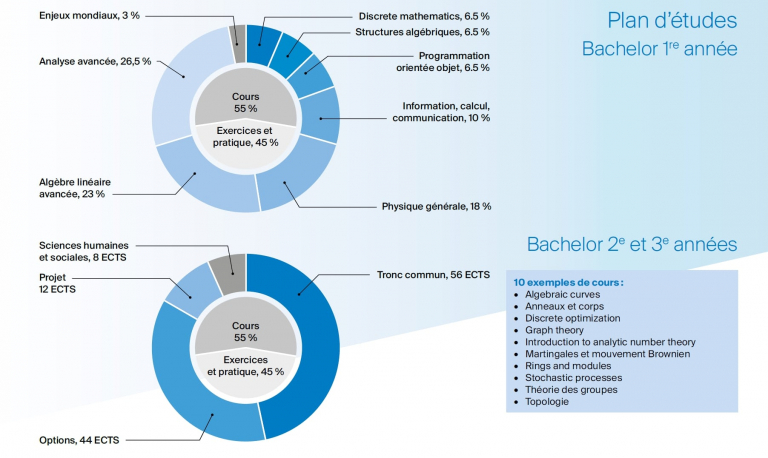
The basics of analysis, geometry, linear algebra, and general physics are acquired during the first year of the Bachelor’s degree. Teaching then continues with the inclusion of new branches such as topology, operations research, probability, statistics, and numerical analysis. During the third year, the students can choose all of their classes. They also carry out two semester projects. Their degree therefore has a personal touch which serves them well in choosing a Master’s program.
Bachelor: simplified study plan
Master: prospects
The Master’s degree in Mathematics focuses on different mathematical fields (algebra, analysis, probability, theory of numbers, geometry, and topology). The level and variety of classes taken enable the students to acquire great skills in fundamental mathematical tools, abstract reasoning, as well as anticipating differing fields of application.
The Master’s degree in Applied Mathematics focuses on the applications of mathematics (operations research, applied probability and stochastic processes, statistics, numerical analysis, and scientific calculation). The students become specialists in analyzing complex problems requiring abstraction, the extraction of relevant parameters, simulations of the system studied, predictions and comparisons of results with reality. This program also includes a semester-long internship in industry.
Other programs are also open after graduating with the Bachelor’s degree, in particular some interdisciplinary Master’s programs.
Further information on Master’s study programs.
Please note that the information regarding the programs’ structure as well as the simplified study plan may be subject to change and that these are no legally binding. Only the official regulations and study plans are binding.
Career prospects

Mathematicians can just as easily be called upon to engage with the evaluation of public policies as to aid the improvement of business management or the creation of industrial products. Mathematicians’ mastery of modelling technics, along with their expertise in statistics and problem solving, affords them professional opportunities in fields as diverse as IT, actuarial science, meteorology, consulting and finance – the latter having been one of the most fertile areas of employment for mathematicians over the past two decades.
Finally, by opting for an academic career and a PhD, graduates could prefer to pursue careers in teaching or research.
Alumni testimony

I moved from Zurich to New York at the beginning of 2014. I had been working for two and a half years for UBS when they offered me the chance to move abroad.
I work at UBS, in New York. I have always liked traveling and discovering new cultures: I grew up in the Italian speaking part of Switzerland, I wrote my Master’s thesis in Australia and I worked in Zurich. The day my boss asked me if I wanted to move to New York for two years, I took the opportunity.
I love challenges. When I graduated from EPFL, I had two job offers: one in the industry and another in finance. I chose finance. It gave me the possibility to live in Zurich and to learn the third national language, and the economic crisis made this field even more challenging for me.
At UBS, I work as a quantitative risk analyst. In other words, I develop methods to analyze the risk that the bank takes when it gives credits to its customers. I define scenarios to see how the portfolio of a client changes in different situations. Since I have been in New York, I not only implement the methods that we develop in Switzerland, but I also explain the functionality of the models and the outputs to the people who are going to use them and analyze the data. I therefore often interact with my colleagues, our stakeholders and the IT department.
The quantitative methods I acquired during my studies are very useful. When I develop or improve models for example, I need my background in mathematics. But what is very important too, is that EPFL taught us how to work: how to think, how to structure pieces of information, how to search for the data you need.
I will decide in two years if I want to stay longer in the USA or not. But in any case, this experience has been absolutely unique for my career and my personal life.
Contact
To learn more about this program, please use the following contacts:
+41 21 693 25 65